人工智能导论

[TOC]

第三章图搜索与问题求解

搜索的类型：

  • 按是使用启发式信息

    • 盲目搜索：按预定的控制策略搜索，搜索过程中获得的中间信息 不改变控制策略

      eg：广度优先搜索、深度优先搜索、有界深度优先搜索

    • 启发式搜索：搜索时加入了与问题有关的启发性信息，指导搜索 朝最有希望的方向前进，加速问题的求解过程并找到最优解

      eg：启发性信息和估价函数、A算法和A*算法

  • 按问题的表示方式

    • 状态空间搜索：用状态空间法求解问题进行的搜索
    • 与或树搜索：用问题归约法求解问题进行的搜索 ==（不学，知道有即可）==

状态图搜索

状态图：描述问题的有向图称为状态空间图，简称状态图

基本思想：

  • 将问题的初始状态作为当前节点进行扩展，生成一组子节点

  • 然后检查问题的目标状态（节点）是否出现在这些子节点中。

    • 若出现，则搜索成功，找到了问题的解；

    • 若未出现，则再从已生成的子节点中选择一个节点作为当前节点进行扩展

  • 重复上述过程，直到目标状态出现在子节点中，或无可操作节点为止

状态空间搜索算法的数据结构和符号约定

  • OPEN表：记录未扩展(待考察)的节点，存放刚（新）生成的节点。

  • CLOSED表：记录已扩展(考察过)的节点，存放已扩展节点。

  • S：问题的初试状态。（起始节点）

  • G：搜索过程所得到的搜索图。

  • M：当前扩展节点新生成的、且不是自己先辈的子节点集合

image-20211219165908598

搜索过程如右图image-20211219165943407

盲目搜索小结 ==（盲目搜索基本都学过，省略）==

  • 本质：以初始节点为根节点，按照既（预）定的策略对状态空间图进行遍历，并希望能够尽早发现目标节点
  • 遍历策略是既定的，因此称为盲目搜索、
  • 产生的无用节点较多，效率低，易产生组合爆炸
  • 若能找到一种方法用于排列待扩展节点的顺序，即选择最有希望的节点加以扩展，则搜索效率将会大大提高（启发式搜索）

启发式搜索

启发信息

  • 假设初始状态和目标状态都是完全确定的
  • 从初始状态到目标状态有一个给定空间
  • 问题的关键：如何有效搜索这个给定空间
  • 这种搜索需要某些有关具体问题领域特性的信息，把这类特性信息称为启发信息
  • 利用启发信息的搜索方法叫做“启发式搜索方法”

估价函数

估价函数用来估计节点重要性的函数。估价函数 $f(x)$被定义为从初始节点$S_0$ 出发，约束经过节点 $x$ 到达目标节点 $S_g$ 的所有路径中最小路径代价的估计值。它的一般形式为：
$$
f(x) =g(x)+h(x)
$$

  • $g(x)$是从初始节点 $S_0$ 到节点 $x$ 的实际代价；
  • $h(x)$是从节点 $x$ 到目标节点 $S_g$ 的最优路径的估计代价

全局择优与局部择优

  • 全局择优：寻找OPEN表中全部节点里代价最小的节点进行扩展
  • 局部择优：仅寻找当前扩展节点的子节点中代价最小的节点进行扩展

A算法（启发式搜索算法）：

图搜索算法中，如果搜索的每一步都利用估价函数$f(x)=g(x)+h(x)$对OPEN表中的节点排序，则该搜索算法为A算法。

A*算法

  • 对A算法的估价函数$f(x)=g(x)+h(x)$加上某些限制后得到的一种启发式搜索算法

  • 假设$f^*(x)$是从初始节点S出发经过节点x达到目标节点的最小代价，估价函数$f(x)$是对$f^*(x)$的估计值。且$f^*(x)=g^*(x)+h^*(x)$

  • A*算法对A算法（全局择优的启发式搜索）中的$g(x)$和$h(x)$分别提出如下限制：

    • •$g(x)$是对最小代价$g^*(x)$的估计，且$g(x)>0$
    • •$h(x)$是最小代价$h^*(x)$的下界，即对任意节点n均有$h(n)≤h^*(n)$
    • •即：满足上述两条限制的A算法称为A*算法。

第四章 基于遗传算法的随机优化搜索 ==考计算题==

遗传操作：

  • 选择—复制
  • 交叉
  • 变异

选择—复制

选择种群中**适应度较高的个体(染色体)**进行复制，以生成下一代种群
$$
P(x_i)的计算为:p(x_i)=\frac{f(x_i)}{\sum_{j=1}^{N}f(x_i) }\
f为适应度函数，f(xi)为x_i的适应度
$$
交叉

交叉(crossover)：也称交换(交配或杂交)，即互换两个染色体（个体）某些位上的基因

eg：image-20211219175956280

变异

变异(Mutation)：也称突变，即改变染色体某个(些)位上的基因

eg：image-20211219180055546

遗传算法的操作步骤：

image-20211219180128456

第五章 基于一阶谓词的机器推理

  • 谓词：表达式P(t1, t2, … , tn)称为一个n元谓词，或简称谓词

    • P—谓词名(符号)，表示对象的属性、状态、关系、联系或行为

    • t1, t2, … , t**n称为谓词的项，代表个体对象，有几个就是几元谓词

    • eg：prime(2) ：是一元谓词，表示：2是个素数；

      ​ friend(张三,李四) ：是二元谓词，表示：张三和李四是朋友

  • 函数：（增强谓词的表达能力）

    • 定义： f (x1, x2, … , xn)表示个体x1, … , xn所对应的个体y，称为（n元）个体函数，简称函数，f是函数符号

    • eg：doctor(father(Li))表示：小李的父亲是医生

      ​ equa(sq(x), y))表示：x的平方等于y

  • 约定：

    • 大写英文字母——谓词符号
    • 小写字母f, g, h——函数符号
    • 小写字母x, y, z——个体变元符号
    • 小写字母a, b, c——个体常元符号
    • 谓词中的个体——可为变元、常元，也可为函数

2个量词：表示数量的词

  • **全称量词 $\forall$**：“所有”、“一切”、“任一”、“全体”、“凡是”等词统称为全称量词。

  • **存在量词 $\exists $**：“存在”、“一些”、“有些”、“至少有一个”等词统称为存在量词

5个连词（逻辑运算符）：

  • 合取词∧：表示“并且”，“与”的关系

  • 析取词∨：表示“或者”的关系

  • 蕴涵词→（或“=>”）：表示“如果…则”的关系。如：

    P→Q读作“如果P，则Q”，其中P称为条件的前件，Q称为条件的后件。

  • 否定词$\neg$ （或“～”）：表示“非”，对后面命题的否定

  • 等价词↔或（“<->”）：表示“当且仅当”。

自然语言命题的谓词形式表示 ==应该会考==

  • 首先定义谓词

  • 然后再用连接词把有关的谓词连接起来，形成一个谓词公式

eg：image-20211219182201288

等价谓词公式：

image-20211219182419279 image-20211219182341539

子句集及其化简方法==必考==

定义：

image-20211219182901650 image-20211219182921954

化简方式

  1. 消去蕴含词→和等值词↔
image-20211219183037685
  1. 缩小否定词﹁的作用范围，直到其仅作用于原子公式
image-20211219183102309
  1. 适当改名，使量词间不含同名指导变元和约束变元。即使不同量词约束的变元有不同的名字
image-20211219183229403
  1. 消去存在量词
  • 若该存在量词在某些全称量词的辖域内，则用这些全称量词指导变元的一个函数代替该存在量词辖域中的相应约束变元
  • 若该存在量词不在任何全称量词的辖域内（即它的左边没有全称量词），则用一个常量符号代替该存在量词辖域中的相应约束变元，则可消去该存在量词
  • eg：image-20211219183556194

  1. 消去所有全称量词

    直接删掉

  2. 化公式为合取范式

    使用逻辑等价式

  3. 适当改名，使子句间无同名变元

    对子句集中的某些变量重新命名，使任意两子句间不出现相同的变量名

    eg：image-20211219183914750

  4. 消去合取词∧，以子句为元素组成集合S

eg：image-20211219184044032

应用归结原理求取问题答案 ==可能考==

image-20211219184303793

证明结论时，将结论 非 后，只要能证明有 空子句 出现，即可证明成功

eg：

  1. 证明子句集可不可满足

    image-20211219194453077

image-20211219194501340

  1. 证明谓词公式是否是逻辑结论

    image-20211219194607519
image-20211219194618440
  1. 证明谓词公式是否正确
image-20211219194702289

image-20211219194746906

第六章 基于产生式规则的机器推理

产生式规则的两种形式：

  • $$IF<前件> \quad THEN<后件> \eg:IF \ A \quad THEN \ B$$

  • $$<前件>\longrightarrow <后件>\eg:A \longrightarrow B$$

语义：

  • 如果前提成立或条件满足，则可得结论或执行相应的动作
  • 即后件由前件来触发
  • 前件是规则的执行条件, 后件是规则体

推理网络：相关产生式规则按逻辑关系形成的一个与-或图

eg：image-20211219195556374

产生式系统

产生式系统的三部分：

  • 产生式规则库：描述相应领域知识的产生式规则集
  • 推理机（控制系统）：是一个程序，控制协调规则库与数据库的运行，包含推理方式和控制策略
  • 动态数据库（事实的集合）：存放问题求解过程中当前信息的数据结构（初始事实、外部数据库输入的事实、中间结果事实和最后结果事实）
image-20211219195711531

常用推理算法：

  • 正向推理
  • 反向推理
  • 双向推理

第七章 几种结构化知识表示及其推理

元组

  • 元组（tuple）的数学定义:笛卡尔积中的一个元素(d1,d2,…,d**n)，叫 做一个n元组（n-tuple），简称元组

    • 在关系数据库中，一条记录就是一个元组
    • 元组通常泛指由若干数据项组成的一个整体

  • 三元组的一般表达形式为： (<对象>, <属性>, <值>)或(x,F,v)

  • 三元组可方便地表示简单命题或原子谓词公式

    eg:image-20211219200521224

框架（frame）：一种描述所论对象（一个事物、事件或概念）属性的数据结构

  • 一个框架由若干个被称为“槽”（slot）的结构组成。每一个槽又可根据实 际情况划分为若干个“侧面”（faced）

  • 一个槽用于描述所论对象某一方面的属性

  • 一个侧面用于描述相应属性的一个方面

  • 槽和侧面所具有的属性值分别被称为槽值和侧面值

  • 一般形式：image-20211219200716394

image-20211219200750440
  • 把具体信息填入槽或侧面后，就得到相应框架的一个事例框架

基于框架的推理

  • 基于框架的推理方法是继承
  • 子框架可拥有其父框架的槽及其槽值
  • 实现继承的操作有匹配、搜索和填槽

语义网络

  • 语义网络是知识的一种结构化图解表示

  • 它是由节点和边（有向弧）组成的一种有向图

    • 节点：表示事物、对象、概念、行为、性质、状态等

    • 有向边：表示节点之间的某种联系或关系

    • eg：image-20211219202504569

  • 语义网络可表示事物的属性、状态、行为等

  • 更适于表示事物间的关系和联系

  • 关系（或联系）型的知识和能化为关系型的知识，都可用语义网络表示

  • 常见的几种关系:

    • 实例关系

      • 表示类与其实例（个体）之间的关系
      • 关系“是一个”一般标识为“is-a”，或ISA

      eg:image-20211219202715576

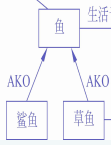
    • 分类（或从属、泛化）关系

      • 指事物间的类属关系
      • 关系“是一种”一般标识为“akindof”或AKO

      eg:image-20211219202817753

    • 组装关系

      • 若下层概念是上层概念的一个方面或一部分，则它们组装关系
      • 其中，关系“一部分”，一般标识为“a-part-of”

      eg:image-20211219202910639

    • 属性关系

      表示对象的属性及其属性值

      eg:image-20211219202943491

    • 集合与成员关系

      • “是……的成员”，表示成员（或元素）与集合之间的关系
      • 关系“是成员”一般标识为“a-member-of”

      eg：image-20211219203031384

    • 逻辑关系

      如果一个概念可由另一个概念推出，两个概念间存在因果关系，则 称它们之间是逻辑关系

      eg：image-20211219203127483

    • 方位关系

      需指出一个事物发生的时间、位置，或它的组成、形状等时，可 用相应的方位关系语义网络表示

      image-20211219203210303

    • 所属关系

      所属关系表示“具有”的意思

      eg:image-20211219203254022

第八章 不确定和不确定性知识的表示和推理

概述

  1. 不确定性信息（uncertain information）

    • 不能确定真实性的信息，eg：
      • 明天下雨
      • 如果发烧且头痛，则患了感冒
    • 上述信息和知识为不确定性信息

  2. 不确切性信息（imprecise information）

    • 不够明确、不够严格（有一定弹性）的信息。例如
      • 小王是个高个子（多高算“高个子”，没有明确的、严格的、刚性的标准）
      • 小明是个好学生
      • 张三和李四是好朋友

  3. 不确定性与不确切性的区别与联系

    • 不确定性信息

      • 不能够确定 真伪 的信息
      • 事件或事物性状、关系或行为 不确定、不肯定

    • 不确切性信息

      • 事物的性状、关系或行为 描述得不够具体、不够严格、不够精确

    • 是 两个相互独立 的信息属性。据此两个信息。信息可分为4种

      • 确定-确切性信息
      • 确定-不确切性信息
      • 不确定-确切性信息
      • 不确定-不确切性信息

  4. 不确定性信息处理与不确切性信息处理

    • 不确定性信息处理解决的是：信息真/伪的可能性问题
    • 不确切性信息处理解决的是：信息真/伪的强弱性问题
    • 从 问题求解 的角度看：
      • 不确定性信息处理解决可能解的问题
      • 不确切性信息处理解决近似解的问题

不确定性知识的表示及推理

不确定性知识的表示

  • 设 $c(S)$ 为命题 $S$ 的可信度，二元组 $(S, c(S))$ 为不确定性命题的表示

  • 不确定性产生式规则 $A\to B$ （第六章）就可表示为
    $$
    (A\to B,c(A\to B)) \quad或\quad A\to (B,c(B|A))\
    c(B|A)表示规则的结论B在前提A为真的情况下为真的可信度
    $$
    eg：如果头痛且发烧，则患了感冒(0.8)

不确定性产生的原因

由于知识的不确定性，在推理过程中引起 结论的不确定性 的 传播情况

  1. 事实（证据）的不确定性：含糊、不完全、随机和模糊等

    • 事实不确定性用可信度 $CF$（certainty factor）值表示
    • eg：非典 $CF＝0.1 CF[0,1]$

  2. 规则的不确定性：专家掌握的 规则是经验性

    • 用可信度CF（certainty factor）表示
    • eg:如果听诊＝干鸣音 则 诊断＝肺炎 CF＝0.5

  3. 推理的不确定性

    推理是 事实(证据) 和 **规则 **结合起来得到结论，反映了不确定性的传播过程

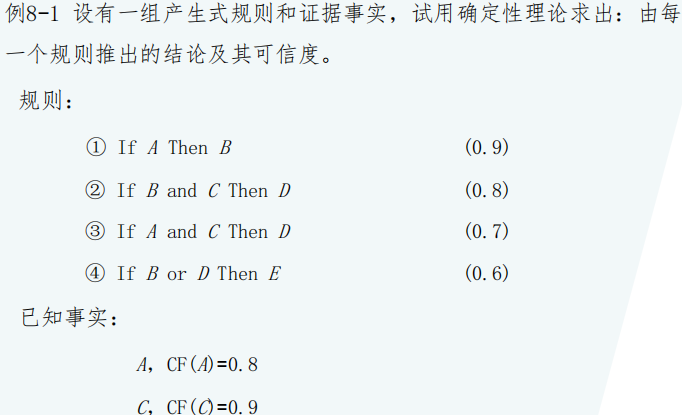
几种经典的不确定性推理模型 ==必考==

事实（证据）间有 “与（and）” 和 **“或（or）” **两种连接形式

  1. And连接时，结论 可信度的计算
    $$
    R:IF\ A\ and\ B\ and\ C …and\ F\ Then\ H \quad CF(R)
    \ 结论H的可信度：CF(H)=CF(R)\times \bf min {CF(A),CF(B)…}
    \ 即CF(E1∧E2∧…∧En)＝\bf min{CF(E1), CF(E2), …, CF(En)}
    $$

  2. OR连接时，结论可信度的计算
    $$
    R：IF\ A\ or\ B\ or\ C… or\ F\ Then\ H\quad CF(R)
    \结论H的可信度：CF(H)＝CF(R) × \bf max{CF(A),CF(B)…}
    \即CF(E1∨E2∨…∨En)＝ \bf max{CF(E1), CF(E2), …, CF(En)}
    $$

  3. 重复结论的CF(H)值计算

    结论 $CF(H)$ 分别由不同的两条规则推出，而得两个可信度 $CF(H)_1$ 和 $CF(H)_2$ ，则最终的 $CF(H)$ 为：image-20211221161910568

考试出题例子：

image-20211221162014766 image-20211221162031079

不确切性知识的表示及推理

基于模糊集合与模糊关系的模糊推理

  • 模糊集合与模糊关系
    • 模糊集合
      • 定义：设U是一个论域，U到区间 [0, 1]的一个映射$μ :U\to [0, 1]$就确定了U的一个模糊子集A
      • 映射μ称为A的隶属函数，记为μ(u)
      • 对于任意的$u∈U， μ_A(u)∈[0, 1]$称为u属于模糊子集A的程度，简称隶属度
      • 模糊集合A一般可表示为：

image-20211225123756552

​ 偶序表示法：image-20211225131038912

​ 行向量表示法：image-20211225131141606

​ Zadeh表示法：image-20211225131148746

  • 模糊关系

    • 定义：集合$U_1, U_2 , …, U_n$的笛卡尔积集$U_1×U_2×…×U_n$的一个模糊子集R，称为 $U_1, U_2 , …, U_n$间的一个n元模糊关系

    • 特别地，**$U_n$的一个模糊子集称为U上的一个n元模糊关系**

    • eg:设 $U={1,2,3,4,5}$，U上“远大于”模糊关系可用模糊子集表示

      image-20211225124646225

  • 模糊集合的运算

    • 可定义模糊集合的交、并、补运算

    • 设：A，B是论域 U 的模糊子集。A，B的交集 $A\cup B$，并集 $A\cap B$ 和补集 $A’$，分别有下面的隶属函数确定：

      image-20211225125009940

    • eg：image-20211225125121344

  • 模糊关系的合成

    • 设有模糊集合 $Q=(q_{ij}){n\times m}$，$R=(r{ij}){m\times l}$，其合成运算为：$S=Q\circ R$ 。其中 $S为n\times l的矩阵$，且：$S= \vee{j=1}^{m} (q_{ij}\wedge r_{jk}) \quad 1\le i\le n,1\le k\le l$

    • eg:image-20211225125804998

  • 模糊集合的代数运算

$$
代数积: \mu_{A B}(x)=\mu_{A}(x) \mu_{B}(x)
\代数和: \mu_{A+B}(x)=\mu_{A}(x)+\mu_{B}(x)-\mu_{A B}(x)
\有界和: \quad \mu_{A \oplus B}(x)=\min \left{1, \mu_{A}(x)+\mu_{B}(x)\right}=1 \wedge\left[\mu_{A}(x)+\mu_{B}(x)\right]
\有界积: \mu_{A \otimes B}(x)=\max \left{0, \mu_{A}(x)+\mu_{B}(x)-1\right}=0 \vee\left[\mu_{A}(x)+\mu_{B}(x)-1\right]
$$

  • eg：image-20211225130210469

模糊推理

  • 是基于模糊规则（即软语言规则）的一种近似推理
  • 模糊规则：前提中的模糊集与结论中的模糊集间的一种对应关系
  • 对应关系是两集合间的一种模糊关系，也可表示为模糊集合
  • 一条模糊规则，转换为一个模糊集合（对于有限集则是模糊矩阵）

第九章 机器学习：符号发现于交互学习

机器学习概述

机器学习的原理：

  • 学习流程：
    • 对于输入信息，系统根据目标 和经验做出决策予以响应，执行相应动作
    • 对目标的实现或任务的完成情况进行评估
    • 将本次输入、响应和评价作为经验，予以存储记录
  • 首次决策 时系统无任何经验
  • 后续决策已有经验积累，经验使系统性能不断改善和提高
  • 学习方式需延伸和发展
    • 经验积累过程中发现规律（知识）
    • 规律（知识）指导系统行为
    • 系统性能会大大改善和提高
  • 学习过程
    • 经验积累过程
    • 知识生成过程
    • 知识运用过程
image-20211221163041619

机器学习分类：

  1. 基于 学习途径 的分类

    • 符号学习

      • 以符号数据为输入，以符号运算为方法

    • 神经网络学习（或连接学习）

      • 以符号数据为输入，以符号运算为方法

    • 统计学习

    • 交互学习

      • 交互学习的典型方法就是强化学习（增强学习）

  2. 基于 学习方法 的分类

    • 归纳学习：即由 特殊到一般 的学习
    • 演绎学习：即由 一般到特殊 的学习
    • 类比学习：基于 类比推理 的学习
    • 分析学习：利用先验知识和演绎推理来扩大样例提供的信息的一种学习

  3. 基于 样本数据特点 的分类

    • 有监督学习（supervised learning，亦称有导师学习）
      • 样本数据为一些由向量 $(x_1, x_2,…, x_n)$ 和 **一个对应值y **组成的 序对
      • 用当前由 $(x_1, x_2,…, x_n)$所求得函数值 $y’$ 与原对应值 $y$ 做比较
      • 然后根据误差决定是否对所选用的函数模型的参数进行修正
      • 以概率函数、代数函数或人工神经网络为基本函数模型
      • 采用迭代计算的方法，来拟合相应的数据集
      • 学习结果为函数（即隐藏于样本数据中的规律）
      • 常用于分类问题和回归问题，以对未知进行预测
    • 无监督学习（unsupervised learning，亦称无导师学习）
      • 样本数据为一些向量(x1, x2,…, xn) （而无对应值y）。
      • 其学习方法就是聚类，即把相似的对象做为一类
      • 学习结果为数据类别，即隐藏于样本数据中的模式（类）或结构
      • 无监督学习被用于聚类问题，也可用于数据降维（dimensionality reduction）和图像压缩（image compression）等
      • 聚类学习和竞争学习都是典型的无监督学习

  4. 基于 数据形式 的分类

    • 结构化学习

      以 结构化数据 为输入，以数据计算或符号推演为方法

      eg:神经网络学习、统计学习、决策树学习、规则学习

    • 非结构化学习

      以非结构化数据为输入

      eg：类比学习、案例学习、解释学习

  5. 基于 学习目标 的分类

    • 概念学习 eg：示例学习

    • 规则学习 eg：决策树学习

    • 函数学习 eg：神经网络学习、统计学习中的监督学习

    • 类别学习 eg：无监督学习

    • 贝叶斯网络学习

    • 等等

几种经典的（符号）学习方法

记忆学习

  • 也称死记硬背学习或机械学习
  • 此方法不要求系统具有对复杂问题求解的能力，即没有推理技能
  • 学习方法
    • 直接记录问题有关的信息
    • 然后检索并利用这些存储的信息来解决问题

示例学习

  • 也称实例学习, 是一种归纳学习
  • 从若干实例(含正例和反例)中，归纳出一般概念或规则的学习方法

eg：image-20211221173410394

演绎学习

  • 基于演绎推理的一种学习
  • 是一种保真变换，即若前提真则推出的结论也为真
  • 学习系统：
    • 由给定的知识进行演绎的保真推理
    • 并存储有用的结论

类比学习

  • 学习过程的主要步骤

    • 回忆与联想：

      遇到新情况或新问题时，先回忆与联想，找出与之相似的已解决的有关问题，以获得有关知识

    • 建立对应关系：

      建立相似问题知识与求解问题间的对应关系，以获得求解问题的知识

    • 验证与归纳：

      检验所获知识的有效性，如有错则重复上述步骤修正，直到获得正确知识

      对正确知识进行推广、归纳等，以取得一般性知识

eg：案例（范例）学习、迁移学习（transfer learning）

解释（分析）学习

  • 解释学习（Explanation-Based Learning, EBL）:

    • 运用领域知识，通过对实例的详细分析来构造解释结构
    • 然后对解释进行推广，以得到关于实例的更一般性描述的学习方法

  • 一般框架：

    • 给定：领域知识、目标概念、训练实例和操作性准则

    • 找出：满足操作性准则的关于目标概念的充分条件

发现学习

  • 系统直接从（数据）环境中归纳总结出规律性知识的一种学习
  • 发现学习也是一种归纳学习，且是一种高级的学习过程

决策树学习 ==可能会考构建决策树==

决策树

  • 也称判定树，是由对象的若干属性、属性值和有关决策组成的一棵树
  • 节点为属性，分枝为相应的属性值，分枝间是逻辑“或”关系
  • 根节点到叶节点的所有节点和边，按顺序连成一条分枝路径
  • 叶节点代表相应分枝的结果，即决策（或分类）

决策树学习的基本方法和步骤：

  1. 选属性，按此属性的不同取值对实例集进行分类
  2. 以该属性为根节点，以其不同取值作为根节点的分枝画树
  3. 考察所得每一子类
    • 若其实例的结论完全相同，则以此结论作为相应分枝末端的叶节点
    • 否则，选取一个非父节点的属性，重复步骤(1)、(2)
    • 迭代，直到所有子集全都满足：实例结论完全相同，而得到所有的叶节点为止

ID3算法（如何选择属性作为结点）

  • 以信息熵为度量，用于决策树节点的属性选择
  • 每次优先选取信息量最多的属性，亦即能使熵值变成最小的属性，以构造一棵熵值下降最快的决策树，到叶子节点处的熵值为0
  • 每个叶子节点对应的实例集中的实例属于同一类

信息熵和条件熵

  • 设S是一个实例集(或子实例集)，A为S中实例的一个属性
  • $H(S)$和$H(S|A)$分别为实例集S的信息熵和条件熵，计算公式如下

image-20211221190846795

​

基于条件熵的属性选择

对一个待分类的实例集S

  • 先分别计算各属性A**j(j=1,2,…,l )的条件熵H(S| Aj)
  • 然后取其条件熵最小的属性A**s作为当前节点

具体题中不用计算，凭直觉选，哪个对结果影响更小，选哪个作为结点

强化学习

  • 强化学习（reinforcement learning，亦称增强学习）

    • 针对智能机器人或更一般的智能体（Agent）
    • 在与环境交互的过程中，获得最优动作决策和最优行动策略（policy，即最 优动作序列）的一种机器学习方法

  • 强化学习所解决的一类问题可描述为:

    • 机器人R和环境E

    • E有若干个不同的状态s1,s2…..sn

    • R执行一动作(action)a后，环境E立刻对其做出评价

    • 给R反馈一个奖/惩值

      image-20211221192036334

  • 实质：对任一非目标状态s，要选择其下一个有利于尽快到达目标状态的最优动作a

第十一章 神经网络学习

人工神经元

  • 人工神经元的性质

    • 多输入单输出
    • 突触具有加权的效果
    • 信息加工是非线性

  • 人工神经元的输入输出关系可描述为：

    • x1、x2、…xn为输入
    • y为神经元的输出
    • w1、w2….wn为权值，即神经元间的连接强度
    • $\theta $为阈值，f(X)为神经元的激活函数
image-20211225114949730

不带激活函数的 单层/多个感知机 只能解决线性可分的问题，解决方法：高等数学中的 不定积分，画曲为止 近似求解 ： 使用激活函数

激活函数的作用：加入非线性因素，使神经网络可任意逼近任何非线性函数

常见的激活函数：

  • 阶跃函数 image-20211225115606825
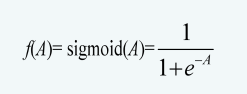
  • Sigmoid函数 image-20211225115617158
  • 分段线性函数 image-20211225115626435
  • 符号函数 image-20211225115711453
  • **双曲正切函数 ** image-20211225115718010
  • **ReLU函数 ** image-20211225115725879

神经网络的拓扑结构

  • 分层前向 网络
  • 反馈前向 网络
  • 互联前向 网络
  • 广泛互联 网络

神经网络的功能

  • 数学上的映射逼近
  • 数据聚类、压缩
  • 联想记忆
  • 优化计算和组合优化问题求解
  • 模式分类
  • 概率密度函数的估计

神经网络学习机理与方法

  • 学习是神经网络的重要特征之一

  • 通过学习/训练，改变其内部状态，使输入/输出呈现某种规律性

  • 学习过程：

    • 将样本数据作为输入/输出
    • 网络按照一定的训练规则，自动调节神经元间的连接强度或拓扑结构
    • 当网络的实际输出满足期望要求或趋于稳定时，则学习成功

  • 学习规则（即权值修正规则）

    • Hebb规则（相关规则）
      • 若相邻神经元i与j同时处于兴奋状态，则它们间的连接强度应加强
      • Hebb规则并未准确反映神经元在学习过程中的突触变化的基本规律
    • δ学习规则（误差修正规则）
      • 根据 实际输出与期望输出的误差 对网络内部进行修改
      • 网络输出均能满足要求

  • 学习方法

    • 根据样例数据的特点，神经网络学习分为：

      • 有监督学习
      • 无监督学习

    • 根据神经网络内部状态的变化，神经网络学习可分为：

      • 权值修正
      • 拓扑变化
      • 权值与拓扑修正

    • 神经网络学习还可分为：

      • 确定性学习

      • 随机性学习

    • 此外还有竞争学习、BP学习、玻尔兹曼学习、迁移学习、深度学习等

神经网络的分类

  • 按网络结构分类

    • 前向（馈）网络
    • 反馈网络

  • 按学习方式分类

    • 有监督（导师）学习网络
    • 无监督（导师）学习网络

  • 按网络的状态分类

    • 连续型网络
    • 离散型网络

  • 按网络的活动方式分类

    • 确定性网络
    • 随机性网络

BP(Back-Propagatino)网络的特点

  • 拓扑结构为分层前向网络

  • 同层节点间不相互连接，层与层之间多采用全互连

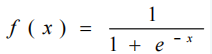
  • 常采用Sigmoid(S型)函数：image-20211225121054737

  • 学习方式为有监督学习

  • 学习算法为δ学习规则, 称为误差反向传播算法：

    • 工作信号正向传播：输入经隐层到输出层，最后形成输出

    • 误差反向传播：从输出层开始，逐层将误差传到输入层，并修改各层连接权值，使误差信号为最小的过程

    • 公式推导思想：修正网络权值与阈值，使误差函数沿梯度方向下降

深度学习

  • 深度学习：基于深度神经网络的神经网络学习或机器学习。
  • 深度神经网络：
    • 含有多个(数个到数千个)隐层的前向（前馈）神经网络。
    • 其隐层可能是：
      • 一行神经元
      • 一行由神经元排列而成的矩阵
      • 一行网络模块，且各层神经元间并非必须为全连接
  • 深度学习的优异效绩归功于以下两点：
    • 自动特征发现（Automating feature discovery）的潜质和特性
    • 采用的“逐层训练，多级学习（抽象）（learning multiple levels of representation）” 等技术技巧

深度学习的发展

  • 深度置信网络和深度卷积网络

  • 深度堆栈自编码网络、深度反卷积网络、深度复卷积网络

  • 稀疏深度网络、深度循环和递归网络、深度生成网络等

  • 复合型的深度网络

    • 深度融合网络
    • 深度贝叶斯网络

  • 深度学习的内涵：“深度”从原来的空间（网络结构）概念扩展到时间（序列）概念

第十二章 数据挖掘与知识发现

数据挖掘

  • 数据挖掘(DM，也称数据开采、数据采掘)：

    • 是KDD过程的一个特定步骤

    • 从数据中提取或挖掘知识

  • 知识发现是从数据中发现有用知识的整个过程(KDD)。

    • 广义的知识发现(KD)

    • 从数据库中的发现知识(KDD)，本章知识发现主要指KDD。

  • KDD过程定义:从数据集中识别出有效的、新颖的、潜在有用的，以及最终可理解的模式的高级处理过程

  • 数据挖掘和知识发现的目的

    • 从数据集中抽取和精化一般规律或模式
    • 涉及的数据形态有：
      • 数值、文字、符号、图形、图像、声音
      • 视频和Web网页等。

  • 数据挖掘与知识发现已成为AI和IT的一个热门领域

  • 应用范围非常广泛，已构成AI技术与应用的一个重要分支领域

    • 企业数据、商业数据、科学实验数据、管理决策数据等
    • 研究内容已相当丰富：如Web挖掘和大数据挖掘

知识发现的一般过程

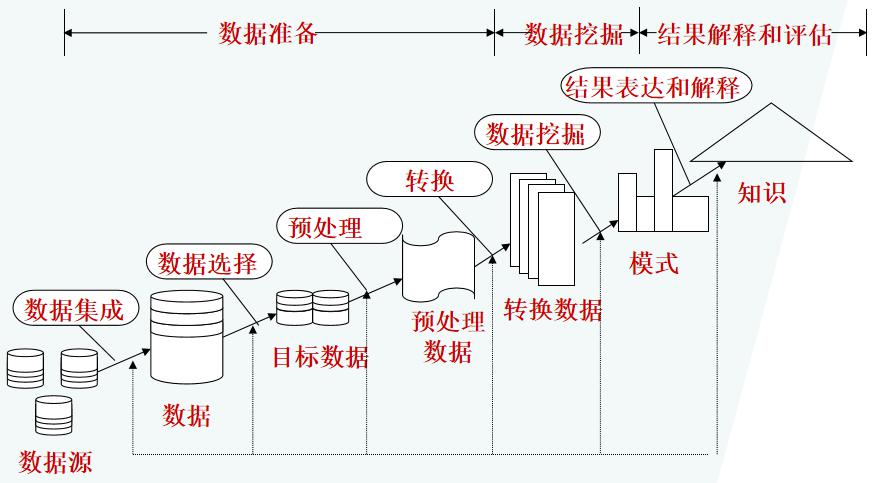
image-20211225121941938

  • 数据准备： 数据选择(data selection)、数据预处理(datapreprocessing)和数据转换(data transformation)

    • 数据选择：确定操作对象，即目标数据(target data)，是根据用户的需要，从原始DB中选取的一组数据。

    • 数据预处理：消除噪声、处理缺值数据、消除重复记录等

    • 数据转换：完成数据类型转换，进行属性约简（从初始属性中找出真正有用的属性，删除无用属性，以减少数据挖掘时要考虑的属性个数）

  • 数据挖掘

    • 首先确定挖掘的任务或目的

    • 确定使用何种挖掘算法

    • **数据发掘的方法 **

      • 数据总结
      • 概念描述
      • 分类
      • 聚类
      • 相关性分析
      • 偏差分析
      • 建模
      • 注意：关联分析、聚类分析、分类、预测

    • 数据挖掘的方法

      • 统计方法
      • 机器学习方法
      • 粗糙集
      • 智能计算方法
      • 可视化

  • 结果的解释与评价

    • 经过评估，剔除冗余或无关的模式

    • 不满足用户要求的模式，需回退到KDD过程的前面阶段

关联规则

关联规则

  • 事件或数据项之间有某种相关性的一种产生式规则。例如：
    • 如果某人买了一台笔记本电脑，则该人还会买一款应用软件。可化为：
    • buys(某人, 笔记本电脑) $\to$ buys(该人, 应用软件) 可简化为：
    • 笔记本电脑 $\to$ 应用软件
  • 这些关联未必是必然的，是一条不确定性规则
  • 为刻画不确定性，引入多种度量

不确定度量

  • 支持度（support）：规则前后件同时出现的概率。

  • 置信度（confidence）：规则前件出现时，后件也出现的概率

  • eg：image-20211225133358962

关联规则的数学定义

image-20211225133539251

  • 支持度和置信度的计算

    image-20211225133638989

K-均值算法

  • 聚类算法：将数据集按数据点间的相似关系划分为若干互不相交的子集，每个子集称为一个簇

  • 数据点的相似性用某种距离（常用欧氏距离）或近似度度量

  • 聚类对数据集的划分原则：

    • 类内对象相似度尽可能大
    • 类间对象相似度尽可能小

  • K-means算法：

    1. 先从样本集中随机选取K个样本做为簇的中心
    2. 计算所有样本与K个簇中心的距离
    3. 对于每一个样本，将其划分到与其距离最近的簇中心所在的簇中
    4. 计算每个簇中心的均值，重新选择一个簇中心，用来更新簇。重复2-4

  • 优点

    • 原理比较简单，实现也是很容易，收敛速度快
    • 聚类效果较优
    • 算法的可解释度比较强
    • 主要需要调参的参数仅仅是簇数k

  • 缺点

    • K值的选取不好把握
    • 对于不是凸的数据集比较难收敛
    • 如果各隐含类别的数据（如数据量或方差）不平衡，则聚类效果不佳
    • 采用迭代方法，得到的结果只是局部最优
    • 噪音和异常点将导致均值偏离严重，对噪声和孤立点比较敏感

聚类与分类的区别？

  • 分类是事先定义好类别，类别数不变。 聚类是指根据”物以类聚”原理，将本身没有类别的样本聚集成不同的组

聚类学习是有监督学习还是无监督学习

  • 无监督学习

均值算法的由来： 质心迭代时，为什么用均值向量作为新质心，就能使质心不再改变而得到

数据集的最佳划分呢？

  • 每个点到所属簇的距离不变

第十六章 专家（知识系统）

什么是专家系统？

  • **专家系统(Expert System,ES)**：能够像人类专家一样解决困难、复杂的实际问题的计算机(软件)系统
  • 专家系统的四个要素（重要特征）：
    • 应用于某专门领域。
    • 拥有专家级知识
    • 能模拟专家的思维
    • 能达到专家级水平

专家系统的结构

  • 专家系统的基本结构

    image-20211225135905153

专家系统的一般结构

image-20211225135827642

  • 知识库（KB）

    • 是ES的知识存储器，存放求解问题的领域知识

  • 数据库

    • 即全局数据库或综合数据库
    • 存储事实、数据、初始状态（证据）和推理的各种中间状态及目标等

  • 推理机

    • 一组控制、协调整个ES的程序。
    • 根据数据库当前的输入数据，利用知识库中的知识，按一定的推理策略

  • 解释模块：

    • 是一组程序，包括系统提示、人机对话、能书写规则的语言 以及解释部分程序

  • 知识库管理系统

    • 把知识加入到知识库
    • 维持知识的一致性及完整性
    • 建立起性能良好的知识库

  • 人机界面

    • 专家系统与外界的接口
    • 系统与外界的通讯与信息交换
    • 必须适应非计算机人员的需求

开发工具

  • 面向AI的程序设计语言
  • 知识表示语言
  • 外壳系统（专家系统工具ESS）
  • 组合式构造工具

知识获取

  • 人工获取

  • 半自动获取

  • 自动获取